عنوان الموضوع : مساعدة في حل تمرين في المعايرة تسيير و اقتصاد
مقدم من طرف منتديات العندليب
اخواني ممكن اجابة على هدا السؤال
هل مقدار التقدم X يساوي مقدار التقدم الاعظمي /2
+
ممكن حل هدا التمرين '''' فقط اخواني ادا لم تستطيعو ان تقرؤا الارقام لا مشكل '''
مصورة بالبورتابل
الله يسلمكم والله راني حاير
وهدا هو التمرين
https://www.shy22.com/pngfile/9tp66659.png
ادخلو على الرابط لتكبير الصور
سلام اخواني
>>>>> ردود الأعضـــــــــــــــــــاء على الموضوع <<<<<
==================================
>>>> الرد الأول :
السلام عليكمــ’’ــ ورحمة الله تعالى وبركاته
صراحة الكتابة نوعا ما غير واضحة لكنني سأحاول فهمها و أقدم لك اجابتي
لي عودة في كتابة الحل
ســلامــ’’ــ
=========
>>>> الرد الثاني :
ســ’’ــــــــلأمـــ
1- انشاء جدول التقدم :
=========
>>>> الرد الثالث :
عبارة التركيز المولي لبيروكسيدات في المزيج :
من جدول التقدم لدينا
ولدينا :
نقوم بتعويض قيمة اكس في المعادلة السابقة
أي تصبح
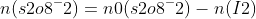
نقسمــ المعادلة على الحجم الكلي و المتمثل في vt (( لا ادري ان كان هذا هو الترميز المكتوب في التمرين لانه غير واضح على العموم الترميز ليس مهم ))
فنحصل على
حيث أن
(( كمية المادة على الحجم = التركيز ))
كما يمكن تقسيم الطرف الثاني إلى مجموع كسرين أي
كتبسيط اكثر
فنجد أخيرا أن
وهو المطلوب
=========
>>>> الرد الرابع :
2- حساب قيمةفي اللحظة t=0 لحظة انطلاق التفاعل
لحظة انطلاق التفاعل : معناه تمـ مزج المحلولين و بالتالي فإن الحجم المعبر عنه هو هو الحجم الكلي (( حجمـ الوسط التفاعلي )) و يساوي 200 ml
c= n0/vt
حيث ان c هو تركيز البيروكسيدات بداية التفاعل
وn0 هي كمية البيروكسيدات الابتدائية
و vtهو الحجم الكلي = 200ml
ولدينا
'' تمـ تحويل الحجم من المليلتر إلى اللتر بالضرب في 10 قوة ناقص ثلاثة ''
و بالتالي نجد : بالتعويض
'' تمـ تحويل الحجم من المليلتر إلى اللتر بالضرب في 10 قوة ناقص ثلاثة ''
=========
>>>> الرد الخامس :
3- أ - يتمــ’ــ تبريد العينات مباشرة بعد فصلها عن المزيج : قصد توقيف التفاعل الحاصل سابقا و المتمثل في تشكل ثنائي اليود
=========
3-ب - كتابة المعادلة الاجمالية لتفاعل الأكسدة الارجاعية :
أولا و قبل كل شيء نكتب المعادلات النصفية : *حيث انه في الطرف الاول نكتب ماهو معطى ففي هذه الحالة لدينا s2o3^-2 كمتفاعل تم وضعه في الوسط بالاضافة إلى انه لدينا ثنائي اليود المتشكل و الذي تحصلنا عليها من التفاعل الأول
ومنه :
معادلة الأكسدة :'' الاكترونات في الطرف الثاني تسمى أكسدة ''
معادلة الارجاع : '' الاكترونات في الطرف الاول تسمى ارجاع ''
،، بما أن الالكترونات متساوية في المعادليتن فيمكننا كتابة المعادلة الاجمالية و ذلك بالجمع بين أطراف المعادليتن النصفيتين فنتحصل على :

تبيين العلاقة بالاستعانة من جدول التقدم :
1- انشاء جدول تقدم المعايرة :
لي عودة لاحقا لاكمال الحل
بارك الله فيك اخي واكثر من امثالك
فقط يا اخي العزيز لو تشرحلي اخر سؤااال في الموضوع
تاع حساب السرعة الحجمية
السلامــ’’ـ عليكمــ’’ــ
تسجيل العودة
++ أنا أخت وليس أخ
على العموم جاري اكمال الحل
2- ايجاد العلاقة :
من جدول التقدم لدينا
أيxe = n0(s2o3^-2)/2.
n0(I2)-xe=0أي xe=n0(I2)l
من العلاقة الاولى و الثانية نجد
n0(I2)=n0(s2o3^-2)/2
جداء الطرفين في الوسطين لنتحصل على
حيث n0(I2)= v*l I2 l
و n0(s2o3^-2)= c.ve
ومنه بالتعويض نجد
نقسم الطرفين على 2v فنجد
وهو المطلوب
بالنسبة لاكمال جدول القياسات فالامر أصبح واضحا فقط قم بتالتعويض و ذلك بتطبيق العلاثة التي تم الحصول عليها في السؤال السابق مع تغيير في كل مرة الحجم v المعطى في الجدول
أما بخصوص الرسم فقط قم بتعيين النقط المتحصل عليها حيث أن محور الفواصل يمثل محور الأزمنة و محور التراتيب يمثل تراكيز ثنائي اليود
أنا لم أرسم المنحنى لكنه حتما سيكون متنازل و ذلك لأن ثنائي اليود هنا يمثل متفاعلا '' أي أنه بصدد الاختفاء و بالتالي من المنطق ان يكون منحناه متنازلا''
- حساب بيانيا سرعة التفاعل عند اللحظة t=20min
اتبع هذه الخطوات عند طرح اسئلة تخص ايجاد سرعة خاصة بمتفاعل ما انطلاقا من منحنى لمتفاعل آخر
أولا نكتب عبارة السرعة الحجمية للتفاعل
v vol = 1/v * dx/dt
ثانيا : نحسب ميل مماس المنحنى في اللحظة المعطاة
أي نقوم بحساب فرق الترتيبين على فرق الفاصلتين
ثالثا ايجاد العلاقة بين ثنائي اليود و التفاعل x
من جدول التقدم لدينا
n(I2)= n0(I2) - xe
بالاشتقاق نجد
n'(I2)=n0(I2)'-x'l
فتحة في الرياضيات يقابلها d(.....)/dt في الفيزياء
كذلك مشتق n0(I2)=0 وذلك لأن n0(I2) عبارة عن عددحقيقي يمكن ايجاد قيمته ومن المعلوم أن مشتق عدد حقيقي يساوي الصفر
و عليه نجد
dn(I2)/dt = 0-dx/dt
نضرب الطرفين يف ناقص واحد
نضرب الطرفين في 1/v
لنجد
بتبسيط أكثر و للتوضيح '' يمكن تمديد خط الكسر ليصبح كسر واحد بما أنه يوجد اشارة جداء ''
نعلم أن n/v=c
ومنه
كتصحيح للعبارة حتى تصبح فيزيائية أكثر عوض أن نكتب c(I2) نكتب l I2l '' بين عارضتين ''
فنتحصل في النهاية على
واضح أن الطرف الثاني للمعادلة يمثل العلاقة الخاصة بالسرعةالحجمية للتفاعل و أن الطرف الأول من المعادلة يمثل ميل المماس الخاص بالمنحنى عند اللحظة المختارة '' t=20min '' مضروب في الناقص
و بالتالي فأن السرعة الحجمية للتفاعل هي ميل المماس في ناقص واحد
تمــ’’ــ و بحمده لااجابة عن الاسئلة
فقط ملاحظة : غدا ساذهب إلى طبيب العيون ههه هه ه هه
ان يوجد هناك اي اشكال بامكانك طرحه و ان تمكنت من معرفة الحل سأضعه ضمن ردودي
بالتوفيق
و السلام


















 رد مع اقتباس
رد مع اقتباس